การค้นหาข้อมูล (Searching)

การค้นหาข้อมูล (Searching)

                ในการค้นหาข้อมูลจะมีความสัมพันธ์กับเทคนิคเกี่ยวกับการจัดเรียงลำดับข้อมูล (Sorting) ซึ่งการค้นหาข้อมูลเป็นกระบวนการเกี่ยวกับการชี้ตำแหน่งของข้อมูลที่อาศัยอยู่ โดยจะอาศัยค่าของคีย์ฟิลด์
(Key-Field) ในการค้นหาข้อมูล ส่วนการจัดเรียงลำดับข้อมูลจะเป็นกระบวนการใช้จัดลำดับก่อนหลังของคีย์ฟิลด์ที่กำหนดไว้ โดยปกติการค้นหาข้อมูลจะต้องมีการกำหนดคีย์ฟิลด์ไม่ซ้ำกัน

- การค้นหาข้อมูลแบบลำดับ (Sequential Search)

                การค้นหาข้อมูลที่มีลักษณะการทำงานอย่างมีลำดับขั้นตอน โดยมีค่าคีย์ฟิลด์ที่ต้องการหาไปปรียบเทียบกับคีย์ของข้อมูลที่จัดเก็บไว้ ตั้งแต่ตัวแรกเรียงลำดับไปทีละตัวจนกว่าจะพบข้อมูลที่ต้องการ หรือเปรียบเทียบไปจนถึงตัวสุดท้าย โดยผลลัพธ์จากการค้นหาข้อมูลจะมีความเป็นไปได้อยู่ 2 คือ

1. พบตำแหน่งข้อมูลที่ต้องการภายในลิสต์(Successful Search)

                    ตัวอย่างการค้นาข้อมูล

                                กำหนดค่าที่ต้องการค้นหา (Target) ต้องการค้นหา 36

2. ไม่พบตำแหน่งข้อมูลที่ต้องการภายในลิสต์ (Unsuccessful Search)

                    ตัวอย่างการค้นาข้อมูล

                                กำหนดค่าที่ต้องการค้นหา (Target) ต้องการค้นหา 95

- การค้นหาข้อมูลแบบไบนารี่ (Binary Search)

การค้นหาข้อมูลแบบไปนารี่ เพื่อแก้ไขข้อเสียของการค้นหาข้อมูลแบบเรียงลำดับ และเป็นวิธีการค้นหาข้อมูลที่รวดเร็วกว่าแบบเรียงลำดับ แต่การค้นหาด้วยวิธีนี้จะสามารถใช้งานได้ก็ต่อเมื่อข้อมูลจะต้องถูกจัดเรียงลำดับให้เป็นที่เรียบร้อยแล้ว

เทคนิคการค้นหาข้อมูลด้วยวิธีนี้

1. กำหนดข้อมูลที่ต้องการค้นหาและทำการเรียงข้อมูลตามความต้องการ เรียงจากมากไปน้อย หรือจากน้อยไปมากก็ได้

2. ทำการแบ่งข้อมูลออกเป็น 2 ส่วน แล้วทำการหาค่ากลาง

3. เมื่อทราบแล้วว่าค่าของคีย์ฟิลด์อยู่ครึ่งแรกหรือครึ่งหลังแล้ว ก็จะนำข้อมูลในครึ่งดังกล่าวทำการหาค่ากลางอีก ทำแบบนี้ไปเรื่อย ๆ จนกระทั้งได้ข้อมูลที่ต้องการ หรือจนกระทั่งไม่สามารถแบ่งข้อมูลออกเป็น 2 ส่วนได้อีกต่อไป

                ดังนั้นโครงสร้างข้อมูลที่จะใช้การค้นหาแบบไบนารี่ได้ดีจะต้องเป็นโครงสร้างที่อยู่ในลักษณะเป็นแถวลำดับ

ตัวอย่างการทำงานของการค้นหาข้อมูลแบบไบนารี่

1)ข้อมูลที่เก็บรวบรวมได้

2)ทำการเรียงข้อมูลโดยเลือกเรียงลำดับจากมากไปหาน้อย

3)คีย์ฟิลด์ที่ต้องการค้นหาคือ 63 ต้องค้นหาค่ากลางเพื่อทำการเปรียบเทียบ

                        3.1) ค้นหาค่ากลางครั้งที่ 1 ข้อมูลทั้งหมดมี่ 16 คีย์ฟิลด์ ปกติก็จะนำมาทำการหาร 2 จะได้ค่าค่ากลางจะอยู่ในตำแหน่งที่ 8 โดยส่วนใหญ่ก็จะไล่จากค่าน้อยที่สุดไปหาค่าที่มากที่สุด จะนับจากขวามาซ้าย ดังนั้น 8 ก็คือ 68 ส่วนใหญ่จะเลือกค่าที่ต่ำไว้ก่อน

           3.2) ค้นหาค่ากลางครั้งที่ 2 ซึ่งค่าของคีย์ฟิลด์จะอยู่ครึ่งหลังเนื่องจาก 63<68 เห็นว่าจะเหลือข้อมูลเพียง 7 คีย์ฟิลด์เท่านั้น เพราะฉะนั้นค่ากลางเท่ากับ 15 ซึ่งอยู่ในตำแหน่งที่ 4 ของข้อมูลที่เหลืออยู่

                                 3.2) ค้นหาค่ากลางครั้งที่ 3 ข้อมูลถูกตัดออกเหลือเพียง 3 คีย์ฟิลด์เท่านั้น ค่ากลางเท่ากับ 63 ซึ่งอยู่ในตำแหน่งที่ 2 ของข้อมูลที่เหลืออยู่ ซึ่งก็จะเป็นค่าคีย์ฟิลด์ที่ต้องการหา ดังนั้นการค้นหาข้อมูลจึงเป็นอับจบกระบวนการ

- การค้นหาข้อมูลแบบไบนารีเสิร์ชที (Binary Search Tree)

โดยทั่วไปแล้วจะมีลักษณะคล้ายต้นไม้ซึ่งแตกกิ่งก้านสาขา และในแต่ละโหนด (ที่อยู่ของข้อมูล) สามารถแยกออกได้เป็น 2 ทิศทาง ซึ่งอาจเรียกว่าเป็นแขนหรือกิ่งของโหนด (Node) คือ กิ่งทางด้านซ้ายมือ (Left Subtree) และกิ่งทางด้านขวามือ (Right Subtree) จะสามารถค้นหาข้อมูลได้อย่างรวดเร็วคล่องตัว และง่ายต่อการจัดการ ซึ่งค่าของข้อมูลแต่ละกิ่งของโหนดจะถูกระบุอย่างชัดเจน

                + กิ่งหรือแขนทางด้านซ้ายมือของโหนด จะต้องมีค่าข้อมูลน้อยกว่าค่าของโหนดปัจจุบัน

                + กิ่งหรือแขนทางด้านขวามือของโหนด จะต้องมีค่าข้อมูลมากกว่าค่าของโหนดปัจจุบัน

                วิธีการค้นหาข้อมูลที่เก็บอยู่ในรูปของไบนารี่ ซึ่งอาจสามารถเดินทางไปตามโหนดที่ชี้ไปตามทิศทางต่าง ๆ เพื่อค้นหาค่าของที่ต้องการ โดยกำหนดให้สามารถเดินทางผ่านแต่ละโหนดเพียงครั้งเดียวเท่านั้น ที่เราเรียกว่าเป็นการเดินทางแบบ Tree Traversal ส่วนวิธีที่จะใช้ในการเดินทางผ่านโหนดต่าง ๆ ได้แก่

   + วิธีการแบบอินออร์เดอร์ (In-order) จะเริ่มเดินทางจากทางซ้ายมือไปที่ Root แล้วกลับไปทางขวาตามลำดับ

  + วิธีการแบบพรีออร์เดอร์ (Pre-order) จะเริ่มต้นการเดินทางจาก Root แล้วตัดไปที่ Subtree ทางด้านซ้ายมือแล้วตัดไปทางด้าน Subtree ทางด้านขวามือตามลำดับ

  + วิธีการแบบโพสต์ออร์เดอร์ (Post-order) จะเริ่มจากทางด้านซ้ายตัดไปทางด้านขวาแล้วจึงกลับไปยัง Root ตามลำดับ

- การค้นหาข้อมูลแบบไบนารีเสิร์ชทรีที่มีความสูงสมดุล (Height Balanced Binary Search Tree)

                การทำหรือการสร้างให้ต้นไม้มีความสมดุลทางด้านความสูงนั้น เป็นการทำให้ต้นไม้ที่สร้างขึ้นเกิดความแตกต่างของระดับของแขนหรือกิ่งทางด้านซ้ายมือ และทางด้านขาวมืออยู่เพียงหนึ่งโหนดเท่านั้น หรือมีระดับของแขนหรือกิ่งทางด้านซ้ายมือและทางด้านขวามือที่เท่ากัน กล่าวคือ

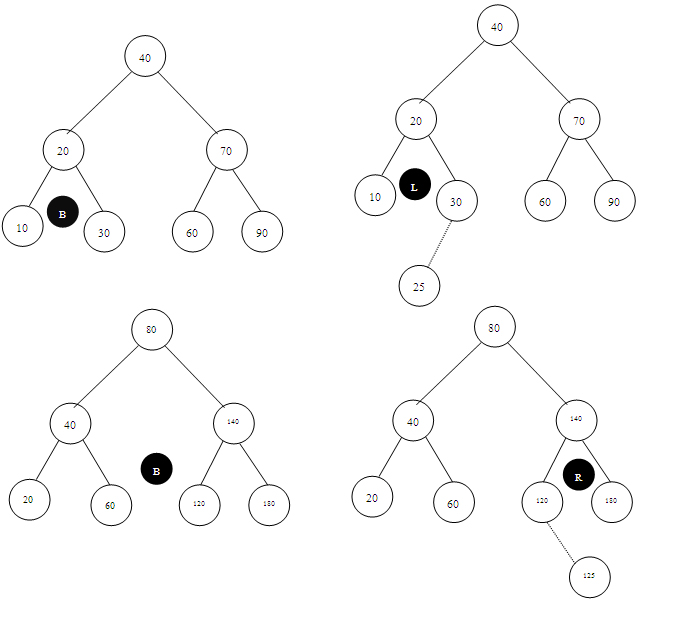
1. LEFT(L) แสดงให้เห็นถึงระดับความยาวทางด้านซ้ายมากกว่าทางด้านขวา ซึ่งอาจเรียกว่า สถานะเอียงไปทางซ้าย

2. BALANCE(B) แสดงให้เห็นถึงระดับที่เท่ากันของทั้ง 2 ด้าน คือ ทางด้านซ้ายและทางด้านขวามือเท่ากัน

3. RIGHT(R) แสดงให้เห็นถึงระดับความยาวทางด้านขวามากกว่าทางด้านซ้าย ซึ่งอาจเรียกว่า สถานะเอียงไปทางขวา

                ดังนั้น ถ้าหากนำโหนดใหม่เพิ่มเข้าไปในต้นไม้ที่สมดุลแล้ว อาจทำให้เกิดการเปลี่ยนแปลงของตัวบ่งชี้ของความสมดุล ซึ่งสามารถแบ่งพิจราณาได้เป็น 2 กรณี ดังนี้

1. ตัวบ่งชี้เดิมอยู่ในรูปแบบ “B” แต่อาจที่จะเปลี่ยนเป็น “L” หรือ “R” นั้นหมายถึงอาจทำให้มีน้ำหนักเอียงไปทาง ซ้าย(L) หรือ ขวา(R) ก็ได้

                  2. ตัวบ่งชี้เดิมอยู่ในรูปแบบ “L” หรือ “R” แต่อาจที่จะเปลี่ยนแปลงเป็น “B” เป็นการทำให้น้ำหนักที่เอียงอยู่สามารถทำให้การเอียงนั้นหมดไป

  

ในกรณีที่ความสูงของทรีไม่สมดุล เนื่องจากโหนดตัวใหม่ที่เพิ่มขึ้นมาทางทิศเดียวกันกับสถานะที่โหนดนั้นเอียงอยู่แล้ว ซึ่งเราเรียกเหตุการณ์นี้ว่า โหนดวิกฤติ (Critical Node)

 

  

                   

           เมื่อเกิดโหนดวิกฤติขึ้นจะต้องทำการแก้ไขโดยการจัดความสมดุลของต้นไม้ใหม่ ด้วยวิธีเปลี่ยนตำแหน่งหน้าที่ ซึ่งอาจจะเปลี่ยนจากสถานะลูกกลายเป็นสถานะพ่อทันที

  

 - การค้นหาข้อมูลแบบแฮชชิ่ง (Hashing)

                เป็นวิธีที่ดีที่สุดสำหรับการค้นหาข้อมูลแบบไบนารี่ โดยใช้เวลาในการค้นหาข้อมูลเป็น O(log₂n) เทคนิคการค้นหาข้อมูลแบบนี้จะทำได้ง่ายและรวดเร็ว โดยการกำหนดเป็นสัญลักษณ์ H(K) ซึ่งค่า K หมายถึง คีย์ที่จะใช้ในการค้นหาข้อมูล โดยทั่วไปฟังก์ชั่นการแฮชชิ่งที่นิยมใช้กันมากและเป็นมาตรฐานหลัก คือ

1.  วิธีการหาร (Division Method) ซึ่งวิธีปฏิบัติจะนำค่าของคีย์ที่เหลือจากการหารแล้วจึงทำการ
บวกเพิ่มค่าด้วย 1 เพื่อทำให้ช่วงของตำแหน่งแฮชชิ่งอยู่ระหว่างค่าที่มีมากกว่าหรือเท่ากับ 1(k ≥ 1) แต่หากไม่ทำการบวกเพิ่มค่าจะทำให้ช่วงของตำแหน่งแฮชชิ่งอยู่ระหว่างค่าศูนย์ถึง จำนวนตัวหาร -1

M            คือ          ตัวหารที่เป็นจำนวนเต็มบวก

X            คือ          ตัวตั้งที่เป็นจำนวนเต็มบวก

1.1)  กรณีไม่เพิ่มค่า: H(k) = X MOD M

1.2)  กรณีเพิ่มค่า(+1): H(l) = (X MOD M) + 1

ตัวอย่างการใช้วิธีการหาร

                ตัวเลขจำนวนหนึ่ง คือ 5368 และสัดส่วนของช่วงห่างในการกระจายเท่ากับ 15 เพราะฉะนั้นการทำ Hashing จะมีค่าเท่าไร

วิธีทำ      สูตร        H(k)          =     (X MOD M) + 1

                                                =     (5368 MOD 15) + 1

                                                =     13+1

                                                =     14

                ดังนั้น ค่า Hashing มีค่าเท่ากับ 14

2.  วิธีการ (Mid Square) เป็นการยกกำลังสองสำหรับค่าของคีย์นั้น และเอาค่าคีย์หลักที่อยู่ตรงกลางของผลลัพธ์มาเป็นค่าของ Address ซึ่งการที่จะเอาค่าคีย์ที่อยู่ตรงกลางมานั้นจะต้องทำการตัดค่าคีย์ที่อยู่ทางด้านซ้ายสุด และทางด้านขวาสุดออกโดยจะต้องกำหนดว่าต้องการตัวเลขที่ใช้ในการ Hashing กี่หลัก แล้วจึงทำการตัดได้

ตัวอย่างการใช้วิธีการ Mid Square

             ตัวเลขจำนวนหนึ่ง ซึ่งมี 3 จำนวน คือ 1325, 9847, 4301 โดยต้องการตัวเลขที่ใช้ในการ Hashing จำนวน 4 หลัก จงหาค่าของการแฮชชิ่งทั้ง 3 จำนวนด้วยวิธีการ Mid Square

วิธีทำ      k                  :       3891                   9847                   4301

                k2               :       15139881         96963409         18498601

                ทำการตัด   :       15139881         96963409        18498601

ดังนั้น    H(k)              =        1398                   9634                   4986

3.  วิธีการพับ (Folding) เป็นวิธีการแบ่งคีย์ออกเป็นส่วน ๆ ซึ่งแต่ละส่วนจะมีขนาดเท่า ๆ กัน แล้วทำการนำค่าของแต่ละส่วนที่เป็นออกมา แล้วจึงนำมารวมกัน (บวกกัน) หลังจากนั้นจะต้องกลับมาพิจารณาว่าได้มีการกำหนดถึงตัวเลขที่ต้องการใช้ในการ Hashing กี่หลัก แล้วจึงพับหรือละตัวเลขที่อยู่ทางด้านซ้ายมือสุด

ตัวอย่างการใช้วิธีพับ

                    ตัวเลขจำนวนหนึ่ง คือ 6598742316478905 ให้ทำการแบ่งตัวเลขออกเป็น 4 ชุดโดยต้องการตัวเลขที่ใช้ในการ Hashing จำนวน 4 หลัก จงหาค่าของการแฮชชิ่งที่ต้องการ โดยใช้วิธีการ Folding

วิธีทำ      k                                 :      6598742316478905

                ทำการแบบค่า k6598 :      7423  1647  8905

                ทำการบวกค่า k          :      24573

ดังนั้น    ค่า H(k)                        =     4573